As adições e subtrações de frações devem respeitar duas condições de operações:
1ª condição: denominadores iguais.
Quando os denominadores são iguais, os numeradores devem ser somados ou subtraídos de acordo com os sinais operatórios e o valor do denominador mantido. Observe os exemplos:
1ª condição: denominadores iguais.
Quando os denominadores são iguais, os numeradores devem ser somados ou subtraídos de acordo com os sinais operatórios e o valor do denominador mantido. Observe os exemplos:
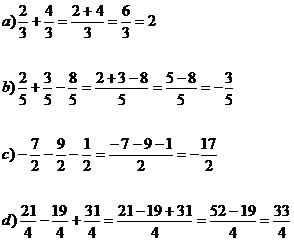
2º condição: denominadores diferentes.
Nas operações da adição ou subtração envolvendo números na forma de fração com denominadores diferentes, devemos criar um novo denominador através do cálculo do mínimo múltiplo comum – MMC dos denominadores fornecidos. O novo denominador deverá ser dividido pelos denominadores atuais, multiplicando o quociente pelo numerador correspondente, constituindo novas frações proporcionalmente iguais as anteriores e com denominadores iguais. Observe os cálculos:
Nas operações da adição ou subtração envolvendo números na forma de fração com denominadores diferentes, devemos criar um novo denominador através do cálculo do mínimo múltiplo comum – MMC dos denominadores fornecidos. O novo denominador deverá ser dividido pelos denominadores atuais, multiplicando o quociente pelo numerador correspondente, constituindo novas frações proporcionalmente iguais as anteriores e com denominadores iguais. Observe os cálculos:
Realizar o MMC entre 3 e 4.
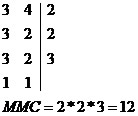
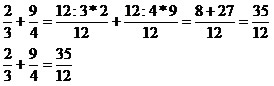
Realizar o MMC entre 5, 9 e 12.
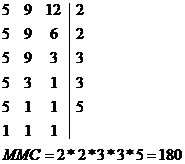
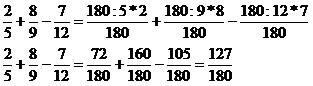
Realizar o MMC entre 15 e 20.
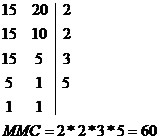
Os números na forma de fração pertencem ao conjunto dos números racionais e são utilizados na representação das partes de um inteiro. Entre as frações, podemos efetuar todas as operações básicas, como adicionar, subtrair, multiplicar, dividir, potencializar e aplicar a raiz quadrada. Dentre os citados, abordaremos os princípios da adição e da subtração de números fracionários.
Nas frações onde os denominadores são iguais, basta conservar o denominador e adicionar ou subtrair os numeradores de acordo com a operação indicada. Por exemplo:
Nas frações onde os denominadores são iguais, basta conservar o denominador e adicionar ou subtrair os numeradores de acordo com a operação indicada. Por exemplo:
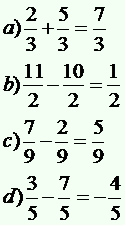
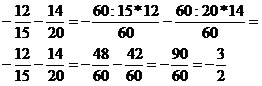
Nos casos de adição e subtração envolvendo frações com denominadores diferentes, devemos realizar a redução ao mesmo numerador. Para isso, devemos aplicar algumas técnicas como a utilização do MMC (mínimo múltiplo comum) entre os denominadores. Após a efetuação do MMC entre os denominadores diferentes, utilizamos o resultado com o novo denominador, que será dividido pelo antigo e multiplicado pelo numerador correspondente. Observe os exemplos:

Essa técnica pode ser utilizada em qualquer adição e subtração de fração com denominadores diferentes, inclusive as frações algébricas. As frações algébricas são aquelas em que a incógnita se encontra no denominador. Observe:
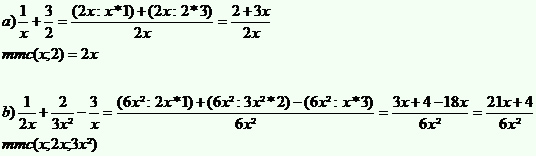
A fração geratriz, quando representada na forma decimal, produz dízimas periódicas simples ou compostas. Portanto, toda dízima periódica (número decimal) deve possuir uma forma fracionária, por isso demonstraremos como transformar números decimais em frações geratrizes. Primeiro vamos observar alguns exemplos de números racionais com períodos:
0,33333333... , período 3 (um algarismo)
0,23232323..., período 23 (dois algarismos)
0,562562562..., período 562 (três algarismos)
Para encontrarmos a fração geratriz seguimos os seguintes passos.
1º passo – relacionar a dízima periódica com uma incógnita
x = 0,333333...
2º passo – multiplicar os dois lados da igualdade por um múltiplo de 10, de acordo com a quantidade de algarismos do período, por exemplo:
um algarismo, multiplicar por 10
dois algarismos, multiplicar por 100
três algarismos, multiplicar por 1000, e assim sucessivamente.
x = 0,333333 ... * 10
10x = 3,3333 ...
3º passo – subtrair a segunda igualdade da primeira igualdade
10x = 3,3333
– x = 0,3333
9x = 3
9x = 3
x = 3/9
Exemplo 2
Encontrar a fração geratriz da seguinte dízima periódica: 0,232323... .
1º passo
x = 0,232323....
2º passo
x = 0,232323 ... * 100
100x = 23,23
3º passo
100x = 23,23
– x = 0,23
99x = 23
99x = 23
x = 23/99
Exemplo 3
Determinar a fração geratriz do número racional 0,562562...
1º passo
x = 0,562562...
2º passo
x = 0,562562... * 1000
1000x = 562,562
3º passo
1000x = 562,562
– x = 0,562
999x = 562
x = 562/999
As frações possuem o objetivo de representar partes de um inteiro, por exemplo, uma barra de chocolate foi dividida em doze partes, as quais nove foram servidas aos convidados de uma reunião. Para representar esta situação devemos utilizar frações, observe:


As partes distribuídas são referentes ao numerador da fração e o inteiro corresponde ao denominador, no caso da barra de chocolate temos numerador igual a 9 e denominador igual a 12. No conjunto das frações é possível estabelecer todas as operações matemáticas: adição, subtração, multiplicação, divisão, potenciação e radiciação. Iremos abordar os casos da multiplicação e divisão, demonstrando as formas mais práticas para a resolução de tais operações.
Multiplicação
A multiplicação de frações é muito simples, basta multiplicarmos numerador por numerador e denominador por denominador, respeitando suas posições. Observe:
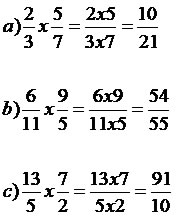
Divisão
A divisão deve ser efetuada aplicando uma regra prática e de fácil assimilação, que diz: “repetir a primeira fração e multiplicar pelo inverso da segunda”.
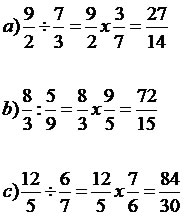
Multiplicação
A multiplicação de frações é muito simples, basta multiplicarmos numerador por numerador e denominador por denominador, respeitando suas posições. Observe:
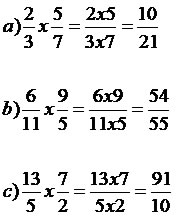
Divisão
A divisão deve ser efetuada aplicando uma regra prática e de fácil assimilação, que diz: “repetir a primeira fração e multiplicar pelo inverso da segunda”.
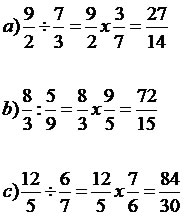
www.mundoeducacao.com.br
muito bom obrigado vc salvou a minha vida e a minha nota,
ResponderExcluirOBRIGADOOOOOO !!!!!!!!!!!
Ooooooooooooobrigada !!! Salvou eu e a minha amiga hahahahah ... #TrabalhoMatemática vllw :3 :p
ResponderExcluir10 ai vou eu
ResponderExcluirnossa obg salvou minha vida recuperaçao ufa passanda
ResponderExcluirEste comentário foi removido pelo autor.
ResponderExcluirNOSSA
ResponderExcluirobrigado você salvou minha recuperação e meu ano